Action 을 선택할때의 기로. Exploitation 하고 말 것인가? Exploration 해볼 것인가?
이전 글 : 검색 - Search Technique
2022.06.13 - [Artificial Intelligence/Reinforcement Learning] - 검색 - Search Technique
검색 - Search Technique
Experience를 얻기 위해 시행한 매우 다양한 trial에서 state 결과를 효과적으로 찾는 방법에 대해 알아보자 이전 글 : 모델결합 학습 [Artificial Intelligence/Reinforcement Learning] - 모델결합 학습 - Integrating Le
skidrow6122.tistory.com
Exploration VS Exploitation
지금까지의 소개 과정에서 action 의 선택 시점에 항상 나오던 개념으로 exploration 과 exploitation 이 함께 등장 해왔다.
일단 두개념의 명확한 정의 부터 해놓고 출발 하자.
- Exploitation : 현재 상황 (알고 있는 정보)에서 판단 해볼 때 가장 BEST Decision 을 선택하고 수행하는 것.
- Exploration : 새로운 시도를 함으로서 새로운 정보를 더 모아 보는 것.
Exploration 의 의미가 조금 와닿지 않을 것이다.
이는 어떤 문제에 대해서 모든 것을 다 알 고 있다면, best decision 이 무엇인지 알 것이고, 그것만 선택 및 사용 (exploitation) 하면 되는데 그러지 않고 새로운 시도를 그냥 한번 해보는 행위를 뜻한다.
사실 현실에서 도 모든 정보를 전지전능하게 다 알 수 있다면, 이 Exploration이 필요 없을 것이나, 보통은 알고 있는 정보가 불충분 하므로 새로운 정보를 얻기 위해서는 새로운 방법으로의 시도가 항상 필요 한 셈이다.
결국 short term 희생을 통해 best long term 전략을 얻는 다는 방법론으로서 exploration 을 한다는 것은 지금당장에 판단 해볼 때는 손실 이지만, 이것을 하다가 좋은 결과를 찾으면 이 좋은 정보를 통해서 결국 exploitation 을 조금더 정확하게 할 수 있기도 하며, 장기적 관점에서는 exploration 하는 것이 조금 더 효율적일 수도 있다.
예를 하나 들어보자.
요즘 나는 점심시간때마다 무엇을 사먹을 지가 가장 큰 고민 거리다. 어느 식당을 가는것이 가장 최적인 지는 매일 선택의 순간 이다.
- Exploitation 을 한다면,,
- 내가 이미 가지고 있는 식당 정보 들 중에 가장 만족스러웠던 식당을 가서 익숙하게 밥을 먹는 것을 선택 한다는 의미이다.
- 내가 가지고 있는 정보 중에서 best 를 선택했으므로 실패 하지는 않지만, 항상 그게 그것인 메뉴를 먹을 수 밖에 없다
- Exploitation 을 한다면,,
- 실패 가능성은 있지만, 더 좋은 식당으로 보이는 식당을 새로 시도해보는 것을 의미한다.
- 아직 경험 해보지 않았으므로 실패 가능성이 있지만, 더 좋은 식당이 얻어 걸릴 가능성이 존재 한다.
결국 우리가 action 을 선택 한다는 것은, 이 두가지 행위를 잘 조합하여 optimization 된 decision을 쫓아 갈 수 있는지에 대한 문제인 것이다.
The Multi-Armed Bandit
상황을 가정 하기 위해서 일단 MDP가 있어야 할 것이다. 이를 위해 우리는 여러개의 슬롯머신 중 어떤 머신의 arm을 당길 것인지에 대한 MDP를 구성 해보자. 이 Multi armed bandit은 현재의 state 는 별로 중요하지 않고, 간단하게 action 과 reward만 의미가 있는 매우 간단한 MDP라고 할 수 있다. 어떤 슬롯머신이건 이를 작동만 시키면 알아서 리턴이 나오는 간단한 환경 이기 때문이다.
따라서 이 MDP의 환경은 tuple <A,R> 로 표현된다.
- A 는 arm을 당기는 m번의 action 을 의미한다.
- 즉, 100개의 동전이 있다면 어느 머신에 동전을 넣고 arm을 당길까 에 대한 것이다.
- Rα(r)=P[r|a] 는 action 에 대한 reward 의 unknown probability distrubution 이다.
- 이 reward function은 reward 를 주는 확률 분포가 모두 다르다고 가정한다. 즉, 어떤 머신은 항상 100원이 튀어 나오는 머신이고, 어떤 머신은 1%의 확률로 100만원이 나오는 환경인 것이다.
- 우리는 이 확률 분포를 모르기 때문에, 매 trial 마다 이거슬 추정하면서 action 을 수행 해 나간다.
- rt≈Rat
- 환경은 reward를 만들어 낸다.
- ∑tτ=1rt
- rt 는 total reward 를 뜻하고, 목표는 이 누적 reward 를 maximize 하는 것이다.
- 누적 reward를 좋게 뽑으려면, 시행 회차 마다 action의 선택이 필요한데, 예를들어 100원을 받았으면, 2회차에서도 해당 머신에서 100원을 계속받을지? 아니면 다른 기계를 선택해서 더 좋은 것을 찾아서 수행할지? 이렇게 확률 분포를 추정 해나가는 것이 필요하다.
- 즉, 100번의 trial 중에 가장 좋은 reward 를 받도록 exploitation 과 exploration 을 적절히 잘 섞어야 한다.
Regret
exploitaton 과 exploration 을 알아 보기전에 각 방법을 펴가하는 방법을 짚고 넘어가야 한다.
Regret 은 어떤 decision을 통해 exploration 또는 exploitation을 하게 되는데, 그 decision을 시행 했을대 원래 있던 optimal한 decision과 얼마의 차이가 있는지? 를 나타내는 개념이다. 즉, option A를 수행 했었어야 하는데 B를 수행 함으로서의 손실을 지표로 나타낸 것이고 우리는 이 regret을 최소화 해야 원하는 목표에 좀 더 가까이 갈 수 있다.
Regret을 수식적으로 알아보자.
- Q(a)=E[r|a]
- state는 따로 없으며 action 만 딱 수행했을 대의 value Q를 나타낸다.
- 여기서 나타내는 기대값은 action value rkqtdmf skxksosek.
- V∗=Q(a∗)=maxQ(a)
- 목표치를 의미하며 현실에서 실제로 구할 수 있는 값은 아니다.
- 모든 학률 분포는 우리가 알 수 없으니, 이 값은 닫ㄴ지 regret 을 정의 하기 위해 만든 값잉라 볼 수 있다.
- lt=E[V∗−Q(at)]
- lt는 regert을 뜻하며, one step에서의 기회비용의 의미를 가지고 있다.
- 이를 해석하면, 현재 step에서 A를 선택 했는데, 원래 B를 선택 했다면 optimal 이었을 시 차이의 기대값이 된다.
여러 trial 을 하다보면 lt 쌓여갈텐데, 이 total regret 은 Lt 로 표현하고 전체 시행횟수 별 regret을 단순히 모두 합쳐둔 값이다.
우리의 궁극적인 목표인 누적 reward를 maximize한다는 것은 곧, 이 total regert을 minimize 한다는 것과 같은 것을 의미한다는 것을 알 수 있다.
ϵ-Greedy Algorithm
ϵ-Greedy 기법은 지금까지의 정리 과정에서 굉장히 많이 등장 해온 개념이다.
일단 MC evaluation 에서 action 별로 추정하는 Q value를 보자.

r_\tau는 action 을 계속 수행 하면서 얻은 reward 들을 의미하고, N_t(a) 로 나누어준 이유는 이 Q라는 것은 시행횟수를 나누어 평균, 기댓값을 도출한 결과 이기 때문이다. greedy 알고리즘은 일반적으로 이 Q 값 중 higheest value를 가진 action을 선택해 나가는 알고리즘 이다.

선택에 딱히 복잡한 메카니즘이 있는 것은 아니고, 단순히 가장 좋은 action 만 선택하는 것인데 exploitation 과 exploration 관점에서만 본다면 그냥 exploitation 만 한다는 의미로 보면 된다. 시행을 거듭 해갈 수록 계속 오차는 쌓여 갈 것이고 regret 역시 계속 증가하는 형태가 될 것이다
ϵ-Greedy 알고리즘은 여기에 ϵ 이라는 파라미터를 하나 더 고려한다. ϵ 이란 확률값에 대한 하이퍼 파라미터로서, action 선택 시 random exploration 할 확률을 강제로 주는 것을 의미한다.
- 1-ϵ : 대부분의 확률이 될텐데, 이만큼의 확률로는 위에서 정의한 greedy 형태로 exploitation 을 수행한다.
- ϵ : 임의로 정의된 이 작은 확률만큼은 랜덤하게 action을 선택하여 exploration 을 수행한다.
도입부에 잠깐 설명하였지만, 항상 가는 식당만 가면 실패 할 확률은 없지만 항상 가던 식당에 안주 할 수 밖에 없는 문제가 있었고, 이를 해결하고자 아주 작은 확률로 다른 action, 즉 다른 식당도 한번씩 가보는 장치를 마련한 것이다.
이 ϵ 을 점진적으로 줄여나가도록 decaying 옵션을 주어 Q값을 정교화 하는 기법도 있다.
이 decaying ϵ-Greedy 기법을 수행 한다면 decaying 파라미터가 추가적인 하이퍼 파라미터가 되며, 이론적으로는 regret이 전체 적으로 어느정도 수렴하는 로그 함수를 그리게 된다고 알려져있다.
Exploration 을 잘 할 수 있는 방법
Optimistic Initialization
샘플링을 통해 Q값을 estimation 할때, 각 actio n이 초기에 굉장히 높은 Q값을 가졌다고 가정해보자. 위에서 정의한 머신 기준으로 보면 N개가 각각 가진 Q값으로 모두 백억씩 설정 했다고 보는 것이다.
초기값을 높이다 보니 1억과 100원의 평균값으로 A 머신의 Q값은 중앙값으로 업데이트 되는 과정이 발생 할 것이다.
그 뒤 똑같이 mc evaluation 을 통해 평균값을 통해 Q값을 계속 업데이트 시켜 나가는 흐름은 동일하게 태워 나갈 것인데, 이렇게 모든 value들을 maximum로 초기화 한 후에 greedy 하게 action 하여 나오는 reward로 평균을 구하여 점점 낮춰나가면, 초반에는 모든 값이 높으니 의도적으로 exploration 을 많이 하는 형태가 만들어 진다.
즉, 의도적으로 초기값을 높게 주어, 초창기에 exploration 을 많이 일어나게 권장하고, 이 과정도 계속 거치다 보면 수렴할 것이며 가면 갈 수록 exploration 확률이 줄어들어 결국에는 decaying ϵ-Greedy 형태가 된다.
개념적으로 이렇게 간단하게 단순히 초기값을 매우 크게 하는 것 만으로도 이런 효과를 가져 올 수 있다.
그렇다면, Exploration 을 할때 단순히 random 하게 action을 선택하지 말고 uncertainty 기준으로 좀 더 잘해 볼 수 있는 방법을 찾아보자.
우선 아래와 같은 세가지 액션을 고려 해 볼 수 있다.

- 초록색 action : action 의 분포가 정확하며 피크값이 높다.
- 파란색 action : action 의 분포가 매우 크고 피크값이 낮다.
이 세가지 액션 중에서는 exploration 을 할때 uncertainty 가 큰 (action의 분포가 매우 크므로 특정하기 어려움) 파란색 action 같은 것들을 먼저 해볼 수 있다.
그래서 파란색의 분포를 조금 더 정확히 추정 한 후 exploitation 하는 방법도 고려해 볼 수있을 것이다.
Upper Confidence Bounds
Uncertainty 를 기준으로 exploration 을 한다는 접근 방법을 위해서는 이 uncertainty 를 estimation 하는 것이 중요하다. 이를 어떻게 유추 할 수 있을까?
결국 불확실성이 높다는 것은 그 action 에 대한 정보가 적다는 것이고, 정보가 적은 이유는 당연히 많이 해보지 않았기 때문이 아닐까? upper confidence ˆUt(a) 를 각 action value마다 정의 하자.
시행 횟수를 N(a) 와 이 upper confidence 값의 관계를 고려 해보면 다음이 성립한다.
- Small Nt(a) ⇒ Large ˆUt(a)
- action 의 시행 횟수가 적으므로 uncertainty 가 높다. estimated value는 uncertain 하다고 할 수 있다.
- Large Nt(a) ⇒ Small ˆUt(a)
- action 의 시행 횟수가 많으므로 estimated value는 accurate 한 편이라고 할 수 있다.
즉, action 의 선택 횟수와 uncertainty 는 반비례 관계이다. 이러한 관점에서 이 Upper confidence bounde (UCB) 를 정의하고 이를 maximize 할 수 있는 action 을 고른다고 해보자.
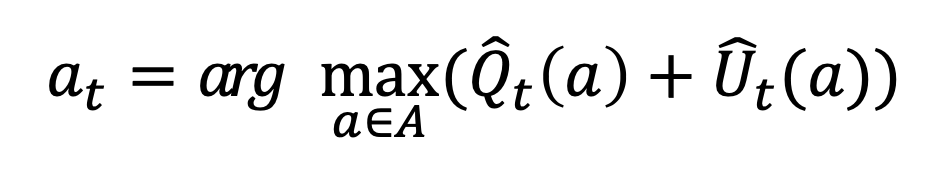
Q는 exploitation 이고, U는 exploration 을 뜻한다고 보면 된다.
estimation 한 Q값과 estimation 한 uncertainty를 합치고, 이 두개의 값이 큰 action 을 선택하는 방법이 된다.
결국 Q값을 가지고 exploitation 을 하는데, 이 방문 횟수를 고려하여 방문이 적은 action 위주로 선택 하겠다는 장치가 됨 을 알 수 있다.
이렇게 하다보면 해당 action에 대한 uncertainty가 줄어 들테고, 그러면 그 액션이 좀 더 정확하게 exploitation 된다는 의미이다.
Thompson Sampling
기존에 action 을 계속 수행해서 얻은 히스토리를 가지고 샘플링을 했었는데, 각각의 action이 다른 action보다 얼마나 maximum Q값을 가질지 확률을 추정해서 그 확률 기반으로 action 을 선택 하는 기법도 있다.
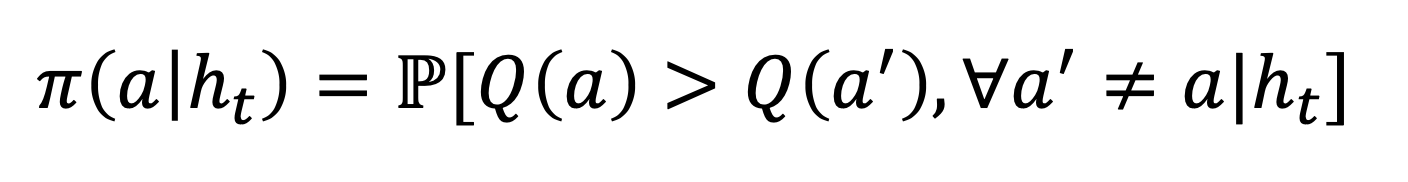
그렇다면 그 확률은 어떻게 계산하는가? Thompson sampling은 이 probability matching 문제를 풀어준다.
결국 지금까지의 히스토리에 대한 posterior distribution 을 알고 싶은 문제가 되는데, 아래의 수식으로 표현된다.
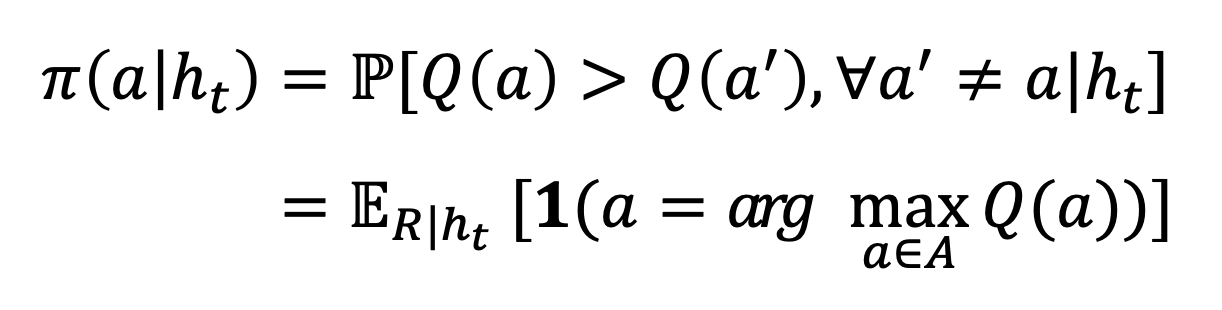
즉, 이때까지의 히스토리에서 베이지안 룰을 활용하여 posterior distribution p[R|ht] 을 계산한다.
그리고 이 posterior 중 에서 reward distribution R을 샘플링 하여 action value function Q를 가상으로 만들어 내는 계산 방식을 따른다.
조금 복잡한데, 요약하면 prior 와 likelihood를 계산해서 posterior 를 만들어 주고, 어떤 확률 분포를 가정하여 그 action에서 어떤 reward가 나올지를 분포 화 해두는 과정이라고 할 수 있다.
그렇다면 우리는 각각의 action마다 자기만의 고유한 reward에 대한 확률 분포가 있을 것이고, 그렇다면 또 어떤 action 을 택했을때 어떤 reward를 받을 수 있을지? 가상의 reward를 만들어 낼 수 있다는 접근인 것이다.
마지막으로 sample 중에 maximize 하는 action at 를 선택하면 되는데, 이제 실제 at를 실행 한다면 Q는 또 업데이트 되고, 업데이트 된 히스토리 ht를 기반으로 또 가상의 시뮬레이션을 통해 확률 분포를 따르는 reward를 뽑거 그것을 가지고 가상의 Q를 또 만들어내고 가장 높은 Q를 가질만한 action 을 또 수행 하는 과정을 반복하는 것이다.
Thompson sampling 은 확률기반으로 샘플링을 하므로 결국 exploration 이 자동으로 수행 된다고 볼 수있다.
왜냐하면 항상 현재의 Q값이 높은 action을 택하는 것이 아니라 가상의 Q를 따르기 때문이다.
모델링을 할때 우리가 가우시안 분포 라고 만약 가정한다면, 실제 문제와 우리가 가정한 모델이 일단 잘 맞아야 하고 샘플링도 잘 되어서 확률 분포가 정확해야만 정확도를 높일 수 있다.
따라서 이 확률 분포를 어떻게 디자인 하느냐가 여기서의 핵심이라 할 수 있다.
전반적으로 ϵ-Greedy 말고 exploitation 하는 기법을 알아보았는데, 각각의 방법의 장단점을 잘 분석해서 문제에 맞는 기법을 잘 선택 해야 한다는 결론에 다다랐다.
지금 까지 강확학습 관련 이론 정리를 쭉 이어왔다.
기본 개념은 어느정도 모두 소개 되었고 강화학습 논문을 큰 허들 없이 읽을 수 있을 정도의 이론은 끝났다고 볼 수 있겠다.
정리 말미로 갈 수록 내용의 정확성이나 논리가 산으로 간 부분도 없지 않아 있어 보이는데, 체력을 좀 보충 하고 틈틈히 수정해 나갈 예정이다.
'Artificial Intelligence > Reinforcement Learning' 카테고리의 다른 글
| 검색 - Search Technique (0) | 2022.06.13 |
|---|---|
| 모델결합 학습 - Integrating Learning and Planning (0) | 2022.06.11 |
| 추정 - Value Function Approximation (0) | 2022.06.06 |
| 모델프리 학습 - Model Free Learning - Control technique on Off-Policy (0) | 2022.06.01 |
| 모델프리 학습 - Model Free Learning - Control technique on On-Policy (0) | 2022.05.30 |




댓글