강화학습에서 이야기 하는 마르코프 모델 (MP, MRP, MDP)에 대해 알아보자
이전 글 : 강화학습 이란?
[Artificial Intelligence/Reinforcement Learning] - 1. Introduction of Reinforcement Learning
1. Introduction of Reinforcement Learning
강화학습이 뭘까? 어떻게 동작하는 것이고, 어떤 개념들의 집합으로 이루어 져있을까? 머신러닝의 기법 중 하나로서의 강화학습 강화학습에 대해 이야기 하려면 머신러닝에 대해 먼저 정의 되
skidrow6122.tistory.com
Markov (마르코프) Property 란 무엇일까?
강화학습의 문제를 푸는 알고리즘이 아닌 문제를 정의 하는 포맷이 되는 기본 개념으로서 현재상태 St 만 알고 있으면, 과거 $S_{t-2}, S_{t-1}$ 을 아는 것과 동일하게 미래 $S_{t+1}$를 추론 할 수 있다는 개념을 의미한다. 다시 말해 미래 상태는 과거와 관계 없이 현재 상태만으로 결정 될 수 있다는 것이다.
즉 현재의 상태 St 는 곧 과거의 history 를 함축하고 있으며, 이 가정을 통해 미래를 충분히 예측할 수 있다는 대전제를 통해 이후 이어질 Markov Process, Markov Reward Process, Markov Decison Process 모델을 가능하게 만든다.
‘상태’와 ‘상태전이확률’ 로만 정의 되는 Markov Process (MP)
Markov Chain 이라고도 불리며, 상태 state 와 다음 상태 state로 전이할 확률만 정의하는 일종의 확률 모델이다. 미래의 이벤트 역시 확률 기반으로 발생하므로 ‘가능한 이벤트의 시퀀스를 설명하는 확률 모델' 이라고 간략히 정의 될 수 있다. 어떠한 agent 의 action 없이 단순히 상태가 전이 될 확률만 정의 되므로 MP는 Markov property 를 갖는 이산확률과정이며, 어떤 마르코프 상태 s와 그 다음 상태 s 에 대해 State transition Probability(상태전이확률) 이 정의 된다고 보면 된다. 이를 간단한 수식으로 표현 하자면 아래와 같다.
$$ P(S_{t+1}=s' | S_0, S_1, ... S_t) = P(S_{t+1} = s'|S_t) = P_{ss'} $$
$S_{t+1}$이 10번째 state라고 가정해보자. 이 10번째 state는 1~9번째 state들에 해당하는 $S_0, S_1, ... S_t$ 에 따르는 조건부 확률로 모델링 되고 이 history state 들은 markov property 라는 대전제에 따라 가장 직전 state 인 $S_t$ 로 함축 되게 된다.
이 대전제는 9번째 history state 역시 1~8까지의 history state 가 낳은 결과라는 체인연결 원리에 의해 성립되며 결국 처음부터 직전 state까지 모두 체크해서 판단하나, 직전 stae 만 체크해서 판단하나 결과는 같음을 의미 한다. 따라서 MP 모델을 간략히 표현 하자면 아래와 같이 set of states 라는 S 와 state transition probability 두가지로 표현 된다고 볼 수 있다.
$$ <S, P_{tran}> $$
이 튜플정보는 다수의 state node 와 각 state node 간 전이 확률이 matrix 형태로 매핑된 state transition probability matrix 형태로 모델링 된다.

MP는 가장 간단한 형태의 모델이며 실제 강화학습의 모델로는 쓰이지 않고, MRP, MDP로 확장하기 위한 세팅으로서만 의미가 있다.
MP에 ‘보상’ 의 개념이 추가 된 Markov Reward Process (MRP)
MRP는 MP를 기본으로 하여 보상(Reward, Return) 이라는 개념이 추가로 정의된 확장 모델이다. 이 Return은 현재 state 에서 state transition 에 따라 받게 되는 reward 와 discounting factor 가 고려된 값으로서, 직관적으로 미래에 받게 될 보상들의 합에 대한 현재 값을 의미 한다. 기존 MP는 현상에 대한 정의만 가능했다면, MRP에서 return 이라는 개념이 고려 되게 됨으로써 진행 한 state transiton 이 좋은 전이였는지 나쁜 전이였는지를 판단 할 수 있게 되고 이것은 곧 ‘가치' 라는 개념의 기준으로 작용 할 수 있게 된다.
MRP를 구성하는 추가 컴포넌트는 아래와 같다.
- Reward $r_t$
- 현 시점 t에서 $s_t$에서 $s_{t+1}$ 로 transition 했을때 얻는 단일 보상 값이다.
- Discounting factor $\gamma \in [0,1]$
- 현재시점에서는 먼 미래에 대한 reward 가 불확실성이 크므로, 현재 상태와 가까운 미래에 더 높은 점수를 주는 철학을 반영한 것으로 0과 1 사이의 값을 보통 적용하여 state 의 진행에 따라 제곱을 증가 시켜 나가지만, Episode 가 반드시 종료 되는 환경에서는 그냥 1을 사용 하기도 한다.
- 또한 return이 무한대로 커지는 것을 방지하기 위한 장치가 되기도 한다.
- Return $G_t = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} ... = \sum_{k = 0}^{\infty} \gamma^k r_{t+k+1}$
- 보상의 총합을 의미한다. 단일 Reward 에 단계별로 discounting factor 가 제곱증가 하여 곱해진다.
- 상술 한 바와 같이, 먼 미래의 Reward는 확률에 따라 못받을 수 도 있으므로 Discounting factor를 곱하여 Reward를 보정하는 효과를 가져다 준다.
- State value function $V(s) = \mathbb{E}[G_t|S_t = s]$
- 현재의 가치를 측정하는 강화학습의 핵심함수로서 reward 들의 총합인 return 의 기대값으로 정의 된다.
- 즉, 이 State value function 으로서 현재 상태의 가치를 판단하게 된다.
따라서 MRP 모델을 표현 하면 아래와 같이 set of states 라는 S와 state transition probability 두가지 기존 MP의 property에 R이라는 Reward function과 $\gamma$ 라는 Discounting factor 가 추가되어 표현 된다.
$$ <S, P_{tran}, R, \gamma> $$
MRP의 transition diagram 은 Reward 가 추가되어 아래와 같이 표현 된다.

정리하면, MRP는 MP에서 state의 전이 가치를 정량화 하기 위해 reward 개념을 도입한 것이고, 이 reward 의 총합인 return 의 기대값으로 현재 상태를 나타낸 state value function이 핵심이라 볼 수 있다.
이 state value function을 계산하기 위해 Bellman Equation 을 사용하고, 이는 state value function V의 재귀적 관계를 표현한 식이며 뒤에 조금 더 자세히 다룰 예정이다.
MRP에 ‘행동’ 의 개념이 추가 된 Markov Decison Process (MDP)
MDP는 MRP를 기본으로 하여 행동(Action) 이라는 개념이 추가로 정의된 확장 모델이며, Action 근원이 곧 Decison 에서 나오므로 Markov Decison Process 라고 한다. 앞선 모델에서 state 가 전이 될때는 단순히 state transition probability 에 의존하여 전이 되었지만 이제는 agent 가 다른 state 로 가기 위하여 다수의 action 중 하나를 선택하여 여러 state 중 하나로 이동 한다는의미로 확장 된다.
따라서 현재 상태의 가치를 판단하는 state value function 역시, 어떤 action 을 선택 했는지에 대한 가치를 판단하는 문제로 확장 되므로 action value function 이라는 확장된 유형의 가치 함수가 활용 된다.
MDP를 구성하는 추가 컴포넌트는 아래와 같다.
- Policy $\pi(a|s) = P(A_{t} = a|S_{t} = s)$
- 선택 할 수 있는 여러개 action 중 어떤 action 을 확률적으로 수행할 것인지를 정의한다.
- $\pi$는 주어진 state s 에서의 action의 확률 분포가 되며 이 policy 에 따라 agent의 행동을 정의 한다.
- Action value function $Q_{\pi}(s,a) = \mathbb{E}{\pi}[{G_t}|S{t} = s, A_{t} = a]$
- 현재상태 s에서 받을 수 있는 리턴의 기대값의 의미는 같은데, a라는 액션을 수행 했을때 라는 조건이 추가된다.
- 좀 더 풀어쓰면, 현재 state 에서 action a를 취한 뒤, 이후 policy $\pi$를 따라 MDP가 진행 될 때의 return의 기대 값이며, 종합하면 현재 정의 된 policy 를 따르 때 현재 상태 s에서 action a를 취하는 행동이 얼마나 좋은 지를 판단하는 값이 된다.
따라서 MDP 모델을 표현 하면 아래와 같이 MRP 모델을 기초로 set of actions 라는 A가 추가되어 표현 된다.
$$ <S, A, P_{tran}, R, \gamma> $$
단, MDP에서도 MRP에서 사용 된 state value function이 사용 되는데, 상태 기준 척도인 state value function과 액션 기준 척도인 action value function은 매우 밀접한 관계를 가지고 있으며, 이 두가지 함수를 수리적으로 풀어가는 방정식이 바로 Bellan equation 이다.

MDP는 복수의 action 과 복수의 state’ 케이스가 고려된 모델로 Sequential Decision Problem, 즉 강화학습 문제를 수학적으로 담아 낸 것이라 할 수 있다. 이 때, MDP에 해당하는 정보를 모두 알 고 있다면 우리는 state 에서 최고의 가치를 가지는 action들을 dynamic programming 방식으로 계산 할 수 있다.
사실 대부분의 현실 세계 에서는 state transition probability 를 모르는데, 강화학습을 토해 reward로 부터 최적의 action을 할 수 있도록 학습이 가능하다.
또한, 이 MDP의 최종 목적은 state value function 과 action value function 을 최대화 하는 policy 를 찾는 것이다.
MP, MRP 그리고 MDP의 관계
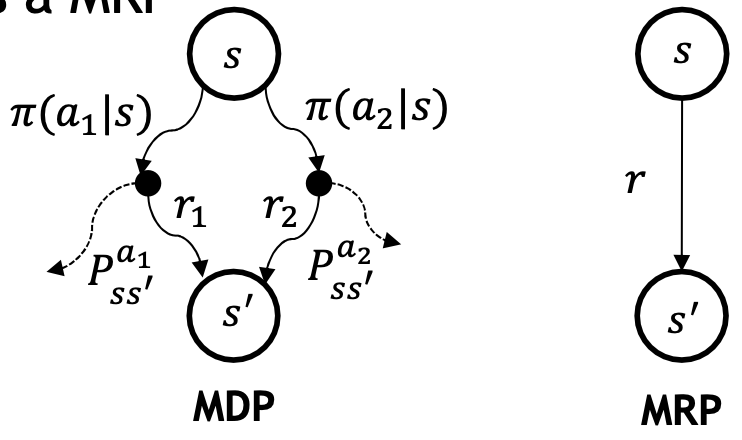
지금까지 정리한 모델은 각 모델 별 property 들을 가지고 아래와 같은 도식으로 표현 된다.
property 들을 상기해보며 각 모델의 관계들을 생각해보면서 정리 내용과 숨은 의미를 복기 해보자.
결론은, MDP 에서 policy 만 도출 해내면 MP, MRP를 충분히 표현 할 수 있다.

강화학습의 기본적인 컨셉을 수리적으로 모델링한 MP, MRP, MDP에 대해 정리 해보았다.
다음 정리에서는 state value function과 action value function 을 활용 하여 최적의 의사결정을 할 수 있어 강화학습의 핵심이라 불리우는 Bellman Equation 에 대해 알아본다.
'Artificial Intelligence > Reinforcement Learning' 카테고리의 다른 글
| 모델프리 학습 - Model Free Learning - Control technique on On-Policy (0) | 2022.05.30 |
|---|---|
| 모델프리 학습 - Model Free Learning - Prediction technique by MC, TD (0) | 2022.05.19 |
| 모델기반 학습 - Model Based Learning - Value, Policy Iteration by Dynamic Programming (0) | 2022.05.17 |
| 벨만 방정식 - Bellman Equation and Optimality (0) | 2022.05.13 |
| 강화학습 개요 - Introduction of Reinforcement Learning (0) | 2022.05.08 |




댓글