MRP, MDP 에서 각 value function 을 활용하여 어떻게 optimality 에 접근 할 수 있을까?
이전 글 : Markov 모델
[Artificial Intelligence/Reinforcement Learning] - 2. Reinforcement Learning Models
2. Reinforcement Learning Models
강화학습에서 이야기 하는 마르코프 모델 (MP, MRP, MDP)에 대해 알아보자 이전 글 : 강화학습 이란? [Artificial Intelligence/Reinforcement Learning] - 1. Introduction of Reinforcement Learning Markov (마..
skidrow6122.tistory.com
Bellman Equation 이란?
Bellman Equation 을 간략히 표현하면, 각각 상태에 대한 value function 기대값을 얻음으로 인해 이것들을 모두 계산하여 최적의 policy (behavior)를 찾는 과정이라 볼 수 있다. 따라서 Bellman Equation 은 강화학습의 최종 Goal 을 찾아가는 핵심적인 개념이며, 요약하면 현재 state와 다음 state` 간 관계를 나타내는 방정식이라 볼 수 있으며 두가지 종류가 존재 한다.
- Bellman Expectation Equation : 반복적으로 기대값을 업데이트 하기 위해서, 현재와 다음의 state 간 value function 사이 관계를 정의. 특정 policy 를 따를 때의 value function 사이의 관계를 의미하고, 모든 state 에 대한 value function 을 반복적으로 업데이트 하여 real value function값을 구한다.
- Bellman Optimality Equation : 가장 큰 value가 높은 value function을 구하는 policy 를 optimal policy 라고 하는데, Bellman Expectation Equation에 맞추어 더 좋은 policy 를 계속 찾아내면 해당 정책이 바로 최적의 정책이다. 이때 최적의 value function 값을 나타내는 것을 optimal value function 이라 하며 그때의 policy 가 바로 optimal policy 가 된다. 바로 이때의 value function 사이의 관계식을 Bellman Optimality Equation 이라 한다.
Bellman Equation 은 미래 상태와 과거 상태들의 sequential 한 관계를 방정식으로 반복해서 풀어 나가는 문제 이므로 Dynamic Programming 을 활용하여 큰 문제를 작은 문제들로 쪼개서 해결해 나가는 방식을 사용 한다. 즉, 각 state 에서의 value function 을 구하고 업데이트 한 후, 업데이트 이후의 value function 을 다시 구하는 방식으로 반복한다.
MRP 에서의 Bellman Expectation Equation
MRP 에서의 핵심은 결국 각 state에서의 가치를 평가하는 것이므로 value function 은 state value function 이 되며, 이는 두가지 파트로 나뉘게 된다.
- 즉시 받는 리워드 rt+1
- 다음 state에서 의 discounted 된 value γV(St+1)
MRP 에서의 state value function 을 직관적으로 생각해보자. 현재 state S 에서의 가치는 사실 어느 방향의 미래로 전이 될지 모르기 때문에 명확히 측정하기 어렵다. 따라서 이러한 전이 방향의 불확실성 때문에 평균을 낸 Expectation value 를 활용 할 수 밖에 없다. 따라서 현재 state 의 V(S) 는 여러 갈래로 전이 했을 때의 reward 의 기대 값이 된다.
MRP의 정의에서 본 state value function 의 수식은 아래와 같으며, 본질적으로 의미하는 바는 특정 state 에서의 리턴의 기대 값이 된다.
- State value function V(s)=E[Gt|St=s]

복잡 해 보이지만, rt+1+γrt+2+γ2rt+3 에 해당하느 term 은 그냥 return (미래 reward 의 합)을 의미 하고 이는 γ 라는 discounted factor로 묶여서 표현된다. 묶고 나서 보면 discounted factor 안에 있는 term 이 곧 다음 state 에서의 return 과 완전 같게 되며. 이는 결국 ‘현재 state 에서의 value function 을 당장 얻을 수 있는 reward 와 그 reward 를 받은 후 전이 된 다음 state 에서의 value function 의 합으로 표현’된다. 가장 마지막에 일반화 된 수식은 사실 s’ 말고도 여러 갈래의 전이 state 가 있으므로 각 state 로의 state transition probability 가 곱해져서 일반화 된 것 뿐이다. (Rs는 그냥 즉시받는 reward.)
이를 매우 간단히 도식으로 보면 다음과 같다.

심은 결국 현재의 value function 은 r 과 v(s’) 의 합으로 구성된다는 것이고, v(s’) 역시 r’와 더 미래의 v(s’’) 의 합으로 계산된 결과라는 점이다.
이 Bellman Equation 은 linear equation 으로 표현 되는 matrix format 을 가진다.
작은 크기의 MRP는 이러한 간단한 linear algebra 문제를 matrix 연산을 통해 풀 수 있지만, 스케일이 크다면 연산량에 문제가 발생하게 되고
- Dynamic Programming : DP
- Monte-Carlo evaluation : MC
- Temporal-Difference learning : TD
와 같은 practical 한 문제 해결 접근 방식을 사용 해 볼 수 있다.
MDP 에서의 Bellman Expectation Equation
문제를 MDP로 확장해보자. MDP 에서는 state value function 에 추가로 action value function 이 추가로 고려 되는데, 역시 현재 받을 수 있는 reward와 다음 state 에서 의 value function의 합으로 표현 되는 것은 동일하다.
- State value function

- Action value function

수식을 뜯어 보면 역시 즉시 받는 reward 와 다음 state 에서의 value function 값의 합인 Gt 가 expectation 안에 풀려서 씌여져 있는 것을 알 수 있다.
양 수식 역시 여러 갈래의 미래 state로의 전이를 고려 하여 state transition probability 롤 적용하여 풀어 보면 아래와 같이 표현 되는데,

action value function 에 해당하는 Qπ(s,a) 를 value function 수식에 대입시키는 형태로 풀어보면 결국 서로가 서로를 표현하고 있다는 점을 알 수 있다.
이를 대입하여 정리하면 아래와 같이 최종 정리 된다.

이는 결국 현재의 value function은 다음 state의 value function 으로 표현 가능 하며, action value function 역시 다음 state의 action value function 으로 표현되는 Bellman Equation 의 핵심 사상을 표현하고 있다.
MDP 역시 간단한 도식으로 보면 아래와 같이 표현 된다.

현재의 value function 은 r 과 v(s’) 의 합으로 구성된다는 것이고, v(s’) 역시 r’와 더 미래의 v(s’’) 의 합으로 계산된 결과라는 점이다.
이제 Optimality 를 고려해보자
리는 강화학습을 통해 최적의 value function 을 얻고자 하므로 optimality 를 고려 할 수 밖에 없다.
‘최적’ 이라는 의미는 결국 모든 policy 에 대해서 value function 을 maximize 하는 value function 을 찾는 것을 의미 한다.
V∗(s)=max
\pi 는 어떤 action 을 선택 할지에 대한 behavior 이고 예를들어 \pi_1은 action a선택에 0.7, b 선택에 0.3을 취하는 policy , \pi_2은 action a선택에 0.9, b 선택에 0.1을 취하는 policy 라 가정 했다면 각 policy 선택히 얻을 수 있는 max \pi 를 선택 하겠다는 것을 의미 한다. 즉, 여러개 정책 중에서 현재 state 의 value function 을 max로 만들어 주는 정책이라고 보면 된다.
action value function의 경우에도 마찬가지로 표현 된다.
Q^* (s,a) = \max_\pi Q_\pi(s,a)
이 두개의 value function 을 구성하는 정책인 \pi 에 주목해보자. optimal policy 는 \pi^*(a|s) 로 설명 할 수 있다 : s 상태에서 a를 선택 하는 가장 최적의 정책
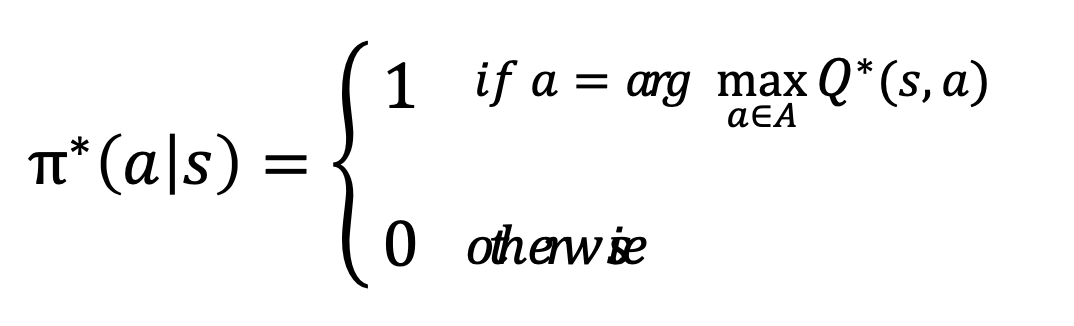
이것은 곧, optimal action value function 을 알고 있다면 그것을 선택하고, optimal 이 아니라면 선택 하지 않는다는 조건부 behavior 를 표현한다고 할 수 있다.
결국은 Bellman Optimality Equation !!!
이제 거의 다왔다. MDP에서 정의한 Bellman Expectation value function 에서의 두 value function 을 최적의 관점에서 고려 해보면 아래와 같다.
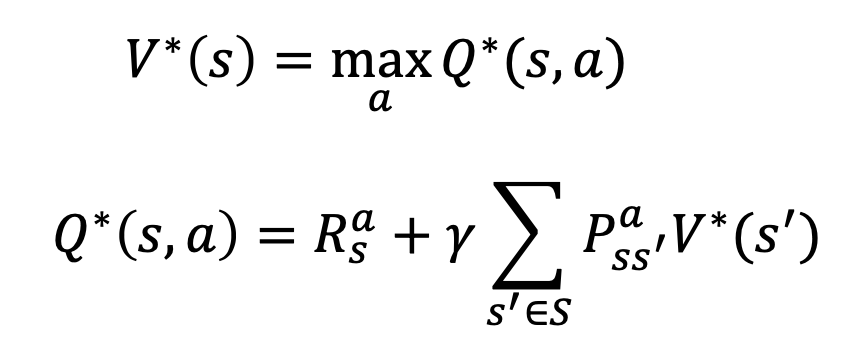
action value function 에 해당하는 Q^*(s,a) 를 value function 수식에 대입시키는 형태로 풀어보면 optimality 관점이 고려된 형태 에서도 역시 서로가 서로를 표현하고 있다는 점을 알 수 있다.
달라진 점은 summation 을 통한 expectation 연산 없이 그냥 최대 값을 가지는 action a 를 선택 하다는 정책이 사용 되었다는 점만 달라 졌다.
이를 대입하여 정리하면 아래의 완성 된 수식이 나온다.
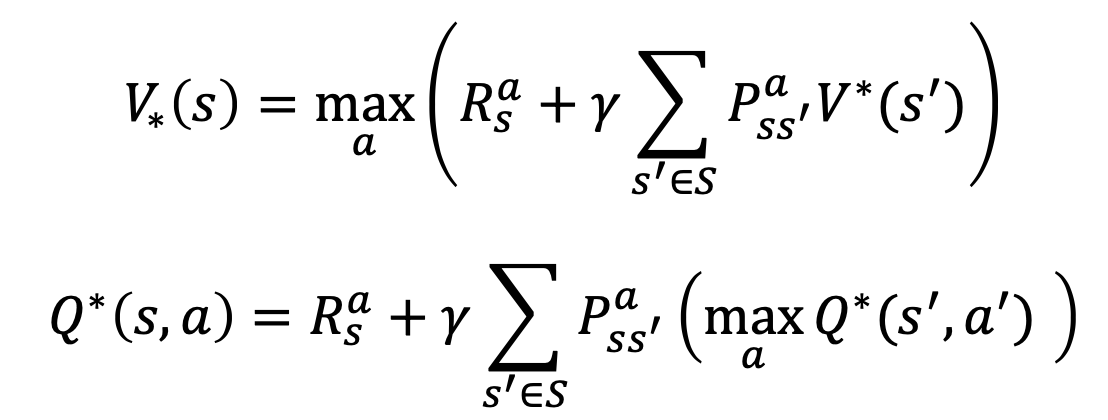
Bellman optimality equation 은 bellman expectation equation 과 달리 max 값을 취한다는 조건이 들어가므로 수식이 linear 하게 풀리지 못한다. 즉 수학적 관점에서 closed 되지 못한 solution 을 찾기 때문에 다수의 반속을 통해 maximize 하는 기법들이 부가적으로 활용 되어야 하며 이는 아래와 같은 여러 테크닉들이 사용 되고 있다.
- Value iteration
- Policy iteration
- Q-learning
- Sarsa
강화학습에서 해답을 찾아가는 Frame이라고도 할 수 있는 Bellman Equation 에 대해 알아보았다. 핵심은 현실이 모델링 된 MDP 문제에서 state value function과 action value function 두 가치 함수들간에 관계성과 optimality 를 찾아가는 접근방식이 결합 하여 학습이 이루어진다는 점을 꼽을 수 있다.
다음 정리에서는 MDP 에서 진짜 optimal 한 value와 policy 즉, value 와 policy 를 maximize 하는 iteration을 수행 하기 위해 기본 접근 방식인 Dynamic programming으로 해답에 다가가는 과정을 다루어 본다.
'Artificial Intelligence > Reinforcement Learning' 카테고리의 다른 글
| 모델프리 학습 - Model Free Learning - Control technique on On-Policy (0) | 2022.05.30 |
|---|---|
| 모델프리 학습 - Model Free Learning - Prediction technique by MC, TD (0) | 2022.05.19 |
| 모델기반 학습 - Model Based Learning - Value, Policy Iteration by Dynamic Programming (0) | 2022.05.17 |
| 마르코프 모델 - Reinforcement Learning Models (0) | 2022.05.10 |
| 강화학습 개요 - Introduction of Reinforcement Learning (0) | 2022.05.08 |




댓글